| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- SQLD 요약
- 백준 1141 로직
- 자바 문자열 예제
- 백준 접두사 자바
- 알고리즘
- SQLD 정리
- 자바 예제
- SQL 기본 및 활용
- 백준 1141
- BFS
- SQLD 내용 정리
- 백준 1141 접두사
- 백준 2293 자바
- 백준 2293 동전 1
- SQLD 책
- 백준 부분합 로직
- SQLD
- SQLD SQL 최적화 기본 원리
- SQLD SQL 활용
- 자바 이분 탐색 예제
- 자바 DP 예제
- 백준
- 오라클 예제
- 백준 동전1 자바
- 너비우선탐색
- 백준 예산 자바
- SQLD 내용
- 백준 접두사 로직
- 백준 2512 자바
- 백준 예산 코드
- Today
- Total
혼자 공부하는 공간
[JAVA] 백준 10868. 최솟값 (세그먼트 트리) :: 로직/코드 - GODZ 본문
안녕하세요 GODZ입니다.
오늘은 세그먼트 트리를 이용한 문제를 풀어볼 예정입니다.
1. 문제
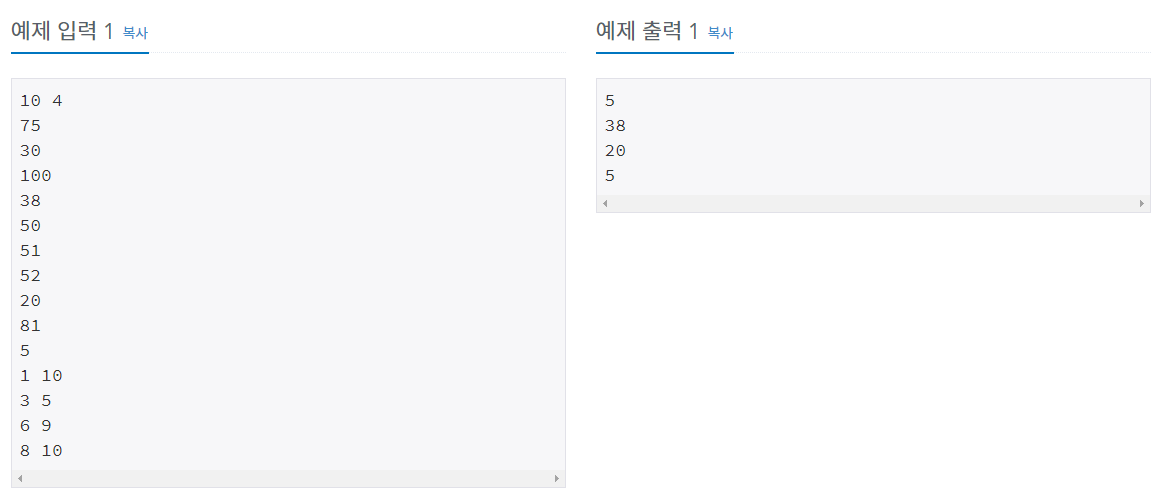
2. 입출력 예제
3. 개념
세그먼트 트리(Segment Tree)는 연속적인 여러 개의 데이터가 존재할 때,
특정 범위 데이터만 처리하기 위해 사용하는 자료구조 입니다.
예를 들어, 배열(arr)에 {10, 9, 8, 7, 6, 5, 4, 3, 2, 1} 이라는 원소가 선형구조로 존재합니다.
여기서 인덱스는 1부터 시작이라고 가정하고 1부터 4, 5부터 8, 3부터 9, 7부터 9 에서의 최솟값을 구하는 기능을 하게끔 만들어야 한다고 합시다.
구현할 때 해당 인덱스(1, 4 // 5, 8 // 3, 9 // 7, 9)를 모두 순회하면서 구해야할 것입니다. 이때 배열 크기가 N, 최솟값을 구하는 횟수가 M 이라면 O(NM)의 시간이 걸립니다.
<세그먼트 트리 적용>
위 예제를 적용해서 세그먼트 트리의 구조를 확인해보겠습니다.
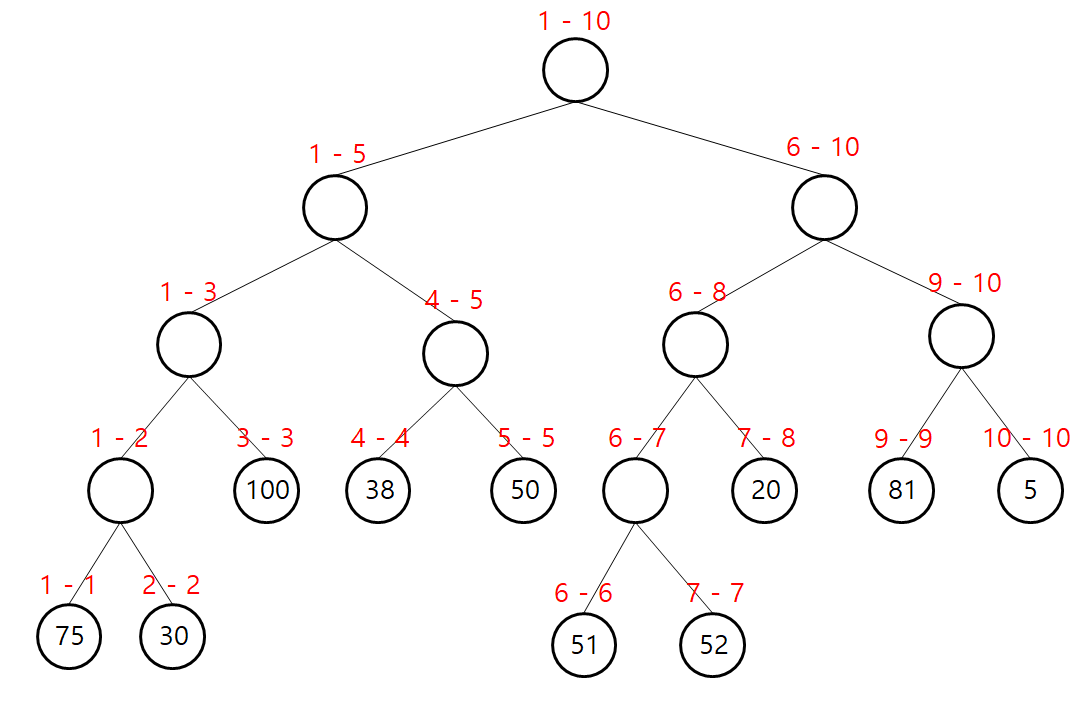
위 그림에서 붉은 텍스트 n - n으로 표시되어 있고, 노드 안에 데이터가 존재하는 노드(Leaf Node)가 바로 배열에 들어있던 데이터입니다.
a - b의 의미는 인덱스 a부터 인덱스 b까지의 최솟값을 의미합니다. 즉 n - n은 결국 인덱스 n에서의 데이터를 의미하겠죠?
1부터 N까지의 전체 범위를 포함하는 것이 Root 노드입니다. 부모의 시작 인덱스와 끝 인덱스의 중간값을 기준으로 적은 쪽을 좌측 자식 노드가, 큰 쪽을 우측 자식 노드가 가져갑니다. 이런식으로 시작과 끝 인덱스가 같을 때 Leaf 노드가 되고, 최초 입력한 데이터를 여기에 넣습니다.
트리의 경우, class를 만들어 구현합니다. (아래 풀이 참고)
배열의 경우, 부모의 인덱스가 idx라면 좌측 자식은 2 * idx, 우측 자식은 2 * idx + 1의 인덱스에 저장됩니다.
그렇기 때문에 배열의 크기 설정은 pow(2, ceil(log2(N)) + 1) 로 설정하면 됩니다. 딱 떨어지게 정확하게 구해도 되지만 마지막 노드의 레벨에 따라서 같게 설정해도 메모리상 큰 차이는 없습니다.
특정 범위의 값을 가지고 올 때는 노드마다 설정된 start와 end 값과 입력에서 들어온 타겟의 start와 end값의 크기를 비교하면서 결정합니다.
예를 들어 (3, 5)의 값이 들어온 경우,
-
start(1)과 end(10)에서 아예 벗어난 경우,
* Integer.MAX_VALUE 처리. -
start(1)과 end(10)을 포함하는 경우,* 해당 인덱스에 대한 값을 바로 반환.
-
전체 범위보다 작은 범위가 겹칠 때,* 좌측 자식, 우측 자식에 대해서 같은 작업 후, 둘 중 최솟값을 반환.
데이터의 수가 N일 때, 결과적으로 세그먼트 트리를 사용할 때와 선형구조를 사용할 때의 차이를 알아보면
-
선형 구조
* 데이터를 변경하는 과정 : O(1)
* 최솟값을 구하는 과정 : O(N)
* 최솟값을 구하는 행위를 M번 진행 : O((1 + N) * M) = O(NM)
-
세그먼트 트리 구조
* 데이터를 변경하는 과정 : O(logN)
* 최솟값을 구하는 과정 : O(logN)
* 최솟값을 구하는 행위를 M번 진행 : O((logN + logN) * M) = O(MlogN)
데이터의 갯수가 많으면 많아질수록 선형 구조와 세그먼트 트리 구조의 효율성 차이는 점점 심해집니다.
4-1. 코드 (Tree 구현)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
/*
* 풀이 1.
* Tree 및 Node class 만들어서 root node를 이용해서 풀이
*/
public class Main {
static int N;
static int M;
static int[] numArr;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine().trim());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
numArr = new int[N + 1];
for(int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine().trim());
numArr[i] = Integer.parseInt(st.nextToken());
}
// Segment Tree Init
SegmentTree sTree = new SegmentTree();
// Root of Segment Tree
SegmentTree.STNode node = sTree.initSegmentTree(numArr, 1, N);
// Query
for(int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine().trim());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
// Get Value For start(l), end(r)
System.out.println(sTree.getVal(node, start, end));
}
}
}
class SegmentTree{
public static class STNode {
int start;
int end;
int val;
STNode leftChild;
STNode rightChild;
}
public static STNode initSegmentTree(int[] a, int l, int r) {
if(l == r) {
// Leaf Node
STNode node = new STNode();
node.start = l;
node.end = r;
node.val = a[l];
return node;
}
// Parent Node
int mid = (l + r) / 2;
STNode lNode = initSegmentTree(a, l, mid);
STNode rNode = initSegmentTree(a, mid + 1, r);
STNode root = new STNode();
root.start = l;
root.end = r;
root.val = Math.min(lNode.val, rNode.val);
root.leftChild = lNode;
root.rightChild = rNode;
return root;
}
static int getVal(STNode root, int l, int r) {
if(root.start >= l && root.end <= r) {
return root.val;
}
if(root.start > r || root.end < l) {
return Integer.MAX_VALUE;
}
return Math.min(getVal(root.leftChild, l, r), getVal(root.rightChild, l, r));
}
}
|
cs |
4-1. 코드 (배열 구현)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
/*
* 풀이 2.
* 배열로 만들어서 풀이
*/
public class Main2 {
static int N;
static int M;
static int[] numArr;
static int[] treeArr;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine().trim());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
numArr = new int[N + 1];
// treeArr Size
int exp = (int) Math.ceil(Math.log10(N) / Math.log10(2)) + 1;
treeArr = new int[(int) Math.pow(2, exp)];
for(int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine().trim());
numArr[i] = Integer.parseInt(st.nextToken());
}
// Segment Tree Init
treeInit(1, N, 1);
StringBuilder sb = new StringBuilder();
// Query
for(int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine().trim());
int targetS = Integer.parseInt(st.nextToken());
int targetE = Integer.parseInt(st.nextToken());
// Get Value For start(l), end(r)
int ans = getMin(1, N, targetS, targetE, 1);
sb.append(ans + "\n");
}
System.out.println(sb.toString());
}
private static int getMin(int start, int end, int ts, int te, int idx) {
if(start >= ts && end <= te) {
return treeArr[idx];
}
if(start > te || end < ts) {
return Integer.MAX_VALUE;
}
int mid = (start + end) / 2;
return Math.min(getMin(start, mid, ts, te, idx * 2), getMin(mid + 1, end, ts, te, idx * 2 + 1));
}
private static int treeInit(int start, int end, int idx) {
if(start == end) {
treeArr[idx] = numArr[start];
} else {
int mid = (start + end) / 2;
treeArr[idx] = Math.min(treeInit(start, mid, idx * 2), treeInit(mid + 1, end, idx * 2 + 1));
}
return treeArr[idx];
}
}
|
cs |
5. 결과


배열로 구현하나, 트리로 구현하나 초기화 과정이나, 최솟값을 찾는 과정은 큰 틀을 벗어나지 않습니다.
배열이라면 Root 노드가 index 1번에 있기 때문에 메소드에서 인덱스 값을 전해주면 됩니다.
트리라면 Root 노드가 다른 노드의 정보를 다 가지고 있기 때문에 Root 노드만 메소드로 전해주고, 노드마다 정해진 start, end 인덱스의 경우도 노드 class가 멤버변수로 갖고 있기 때문에 메소드로 전해줄 필요가 없습니다.