Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- BFS
- 백준 접두사 자바
- SQLD 내용 정리
- 백준 2293 자바
- 자바 문자열 예제
- 백준 부분합 로직
- SQL 기본 및 활용
- 알고리즘
- 자바 이분 탐색 예제
- 백준 2512 자바
- 백준 1141 접두사
- SQLD SQL 최적화 기본 원리
- 자바 DP 예제
- SQLD
- 자바 예제
- 백준 접두사 로직
- 백준 예산 자바
- 오라클 예제
- SQLD 책
- 백준 1141
- 백준 2293 동전 1
- SQLD 요약
- SQLD SQL 활용
- 너비우선탐색
- SQLD 정리
- 백준 1141 로직
- SQLD 내용
- 백준 예산 코드
- 백준
- 백준 동전1 자바
Archives
- Today
- Total
혼자 공부하는 공간
[JAVA] 백준 2512. 예산 :: 로직/코드 - GODZ 본문
안녕하세요 GODZ입니다.
오늘은 이분 탐색을 이용한 문제를 풀어볼 예정입니다.
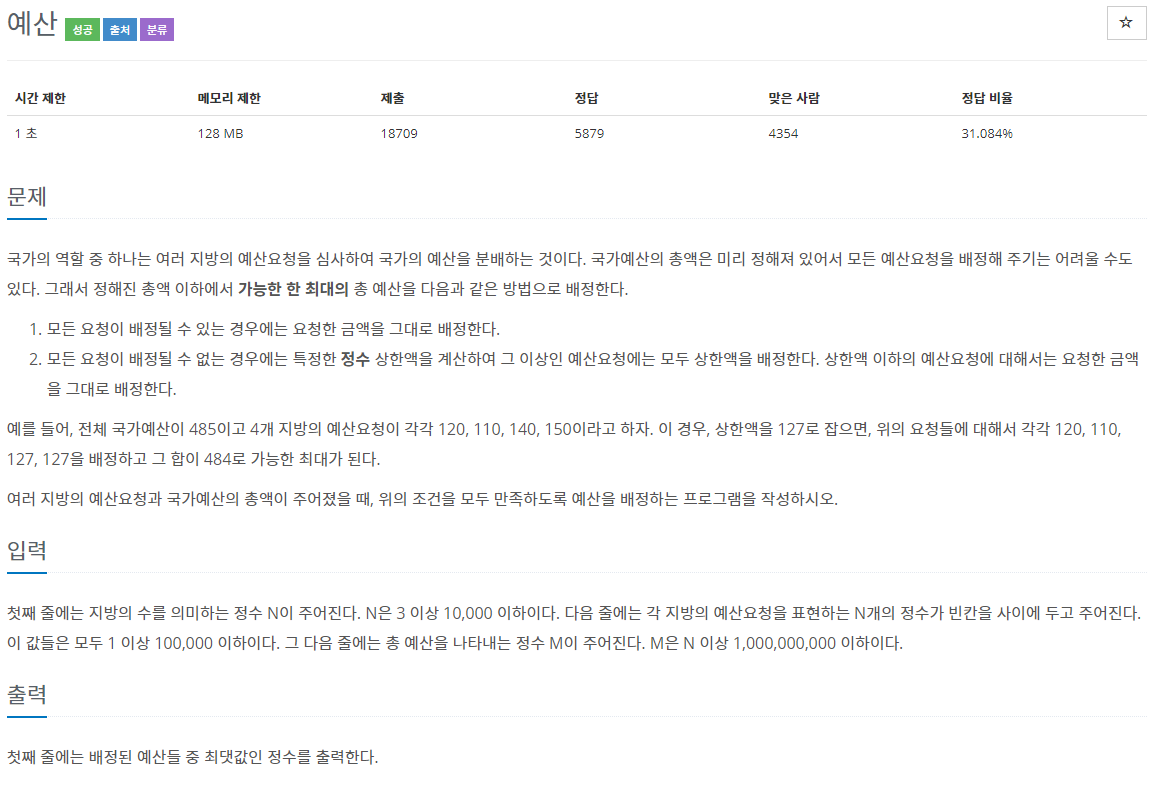
1. 문제
2. 입출력 예제

3. 접근
-
정렬한 뒤, 최대값에서 빼가면서 총 예산(M)을 맞추는 것은 각 예산 값들이 100,000 이하인 것을 감안하면 시간 제한(1초)를 맞출 수 없다.
-
따라서 이분 탐색을 통해 시간 복잡도를 log로 변환하여 작업을 줄이도록 한다.
-
예산의 값 중 최대값을 찾는다.
-
최소값과 최대값의 평균값(mid)을 구해 각 예산에 상한선을 적용한 뒤, 총 예산과 비교한다.
-
총 예산보다 작으면, mid값을 저장하고 mid값을 최소값으로 설정한 뒤 4번 작업 반복.
-
총 예산보다 크면, mid값을 최대값으로 설정한 뒤 4번 작업 반복.
-
-
최대값과 최소값이 같으면 반복을 종료하고, 저장된 mid값 중 가장 큰 값을 출력한다.
4. 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int N;
static int M;
static int nArr[];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine().trim());
N = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine().trim());
nArr = new int[N];
int sum = 0;
int max = 0;
for(int i = 0; i < N; i++) {
nArr[i] = Integer.parseInt(st.nextToken());
sum += nArr[i];
max = Math.max(max, nArr[i]);
}
st = new StringTokenizer(br.readLine().trim());
M = Integer.parseInt(st.nextToken());
if(sum <= M) {
// 모든 요청이 배정될 수 있다
System.out.println(max);
} else {
// 모든 요청이 배정될 수 없다.
int ans = 0;
int min = 0;
int mid = 0;
while(true) {
mid = (max + min) / 2;
sum = 0;
if(mid == min) {
break;
}
for(int i = 0; i < N; i++) {
sum += (mid < nArr[i]) ? mid : nArr[i];
}
if(sum <= M) {
ans = Math.max(mid, ans);
min = mid;
} else {
max = mid;
}
}
System.out.println(ans);
}
}
}
|
cs |
5. 결과

'알고리즘 > 이분 탐색 & 투 포인터' 카테고리의 다른 글
| [JAVA] 백준 1806. 부분합 :: 로직/코드 - GODZ (0) | 2020.09.08 |
|---|
Comments