| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- SQLD SQL 활용
- 백준 부분합 로직
- 백준 1141 로직
- 백준 접두사 로직
- 백준 예산 코드
- 백준 1141 접두사
- SQLD 내용 정리
- 너비우선탐색
- 백준 1141
- SQLD
- SQLD 정리
- 백준
- SQLD 요약
- 백준 2293 동전 1
- 백준 예산 자바
- 자바 문자열 예제
- 자바 이분 탐색 예제
- 백준 2293 자바
- BFS
- SQLD 내용
- SQLD 책
- 자바 예제
- 백준 접두사 자바
- 백준 2512 자바
- SQLD SQL 최적화 기본 원리
- 백준 동전1 자바
- 알고리즘
- SQL 기본 및 활용
- 오라클 예제
- 자바 DP 예제
- Today
- Total
혼자 공부하는 공간
[JAVA] 백준 11724. 연결 요소의 개수(BFS) :: 로직/코드 - GODZ 본문
안녕하세요 GODZ입니다.
오늘은 BFS를 이용한 문제를 풀어볼 예정입니다.
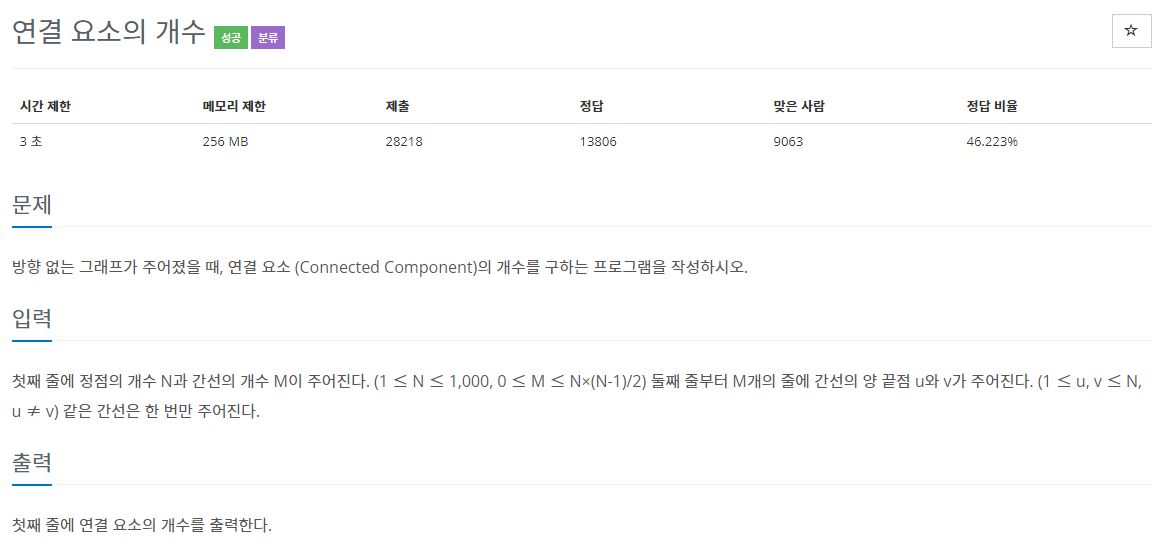
1. 문제
2. 입출력 예제

3. 접근
2020/06/24 - [알고리즘/BFS] - [JAVA] 백준 2667. 단지번호붙이기 (BFS) :: 로직/코드 - GODZ
[JAVA] 백준 2667. 단지번호붙이기 (BFS) :: 로직/코드 - GODZ
안녕하세요 GODZ입니다. 오늘은 BFS을 이용한 문제를 풀어볼 예정입니다. 1. 문제 2. 입출력 예제 3. 접근 단지의 탐색의 종료와 새 단지의 탐색의 시작 사이에 단지 수를 +1 합니다. 각 단지의 집 수�
godzz.tistory.com
위의 문제 기억하시나요?
인접한 칸들을 한 단지로 보고 단지의 갯수를 카운트하는 문제였습니다.
이 문제도 무방향 그래프에서 연결된 정점들을 하나의 구역으로 보고 구역이 몇 개인지 카운트하는 문제입니다.
2차원 배열, 그래프의 차이가 있지만 BFS 로직 자체는 같다고 할 수 있습니다.
여러 시각으로 풀 수 있다고 생각하기에 두 접근방식을 통해 풀어보도록 하겠습니다.
4. 로직


2번 방법을 통해 u, v입력을 끝마치면 i 번 노드의 부모는 arr[i]로 설정이 되어 있습니다.
1번 노드부터 N번 노드까지 반복문을 통해 i번의 노드의 최상위 부모를 찾아 최상위 부모를 Set에 넣으면
Set의 크기가 결국 구역의 갯수가 됩니다.
arr[i]는 단지 i의 부모 노드이므로 최상위 노드를 구하기 위해서는 arr[i] == i 가 될 때까지 재귀호출을 통해 구현합니다.
아래 코드를 통해 확인해보겠습니다.
5. 코드
1. BFS로 구현한 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.StringTokenizer;
public class Main {
static int N;
static int M;
static ArrayList<Integer>[] nodeArr;
static LinkedList<Integer> queue;
static boolean[] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine().trim());
int component = 0;
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
nodeArr = new ArrayList[N + 1];
visited = new boolean[N + 1];
for(int i = 1; i <= N; i++) {
nodeArr[i] = new ArrayList<>();
}
for(int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine().trim());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
// Undirected Graph
nodeArr[u].add(v);
nodeArr[v].add(u);
}
for(int ni = 1; ni <= N; ni++) {
if(!visited[ni]) {
component++;
queue = new LinkedList<>();
solveBFS(ni);
}
}
System.out.println(component);
}
private static void solveBFS(int node) {
queue.add(node);
visited[node] = true;
while(!queue.isEmpty()) {
int currNode = queue.poll();
for(int i = 0; i < nodeArr[currNode].size(); i++) {
int nextNode = nodeArr[currNode].get(i);
if(!visited[nextNode]) {
visited[nextNode] = true;
queue.add(nextNode);
}
}
}
}
}
|
cs |
2. 부모 노드 설정으로 구현한 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Set;
import java.util.StringTokenizer;
public class Main {
static int N;
static int M;
static int[] parent;
static Set<Integer> set;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine().trim());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
parent = new int[N + 1];
set = new HashSet<>();
// 초기화 : 자신의 부모는 자신
for(int i = 1; i <= N; i++) {
parent[i] = i;
}
for(int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine().trim());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
// u와 v의 부모값이 같지 않은 경우
if(getRoot(u) != getRoot(v)) {
// u와 v의 최상위 부모의 값을 찾아
u = getRoot(u);
v = getRoot(v);
// 최상위 부모의 부모로 연결
if(u > v) {
parent[u] = parent[v];
} else {
parent[v] = parent[u];
}
}
System.out.println(Arrays.toString(parent));
}
for(int i = 1; i <= N; i++) {
int p = getRoot(i);
set.add(p);
}
System.out.println(set.size());
}
private static int getRoot(int i) {
if(parent[i] == i) {
return i;
}
return getRoot(parent[i]);
}
}
|
cs |
6. 결과


아무래도 1차원 배열 하나와 Set으로 구현한 2번 방법이 조금 더 효율적인 시간복잡도/공간복잡도를 가지네요.
백준 사이트 특성상 제출마다도 약간의 오차가 있기 때문에 감안하면 별로 큰 수치는 아니네요.
오늘은 여러 관점을 고려해 두 가지 방법으로 풀어보았습니다!
다음엔 또 다른 문제로 찾아뵙겠습니다. :)
'알고리즘 > BFS' 카테고리의 다른 글
| [JAVA] 백준 1697. 숨바꼭질 (BFS) :: 로직/코드 - GODZ (0) | 2020.06.26 |
|---|---|
| [JAVA] 백준 2667. 단지번호붙이기 (BFS) :: 로직/코드 - GODZ (4) | 2020.06.24 |
| [JAVA] 백준 2178. 미로 탐색 (BFS) :: 로직/코드 - GODZ (0) | 2020.06.24 |